Estimating the number of
The process blank protocol used in most chemical processing laboratories consists of processing one blank in parallel with each batch of 8-10 samples. As no sample is added to the process blank, the number of ![]() Be atoms eventually found in it must come either from the
Be atoms eventually found in it must come either from the ![]() Be carrier or from contamination during processing. By analogy with the discussion above, the number of
Be carrier or from contamination during processing. By analogy with the discussion above, the number of ![]() Be atoms in a particular process blank is:
Be atoms in a particular process blank is:
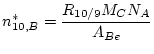 |
(11) |
Now ![]() is the
is the ![]() Be/
Be/![]() Be ratio measured in the process blank and
Be ratio measured in the process blank and ![]() is the mass of Be carrier used in the process blank. The other symbols are as used above. The superscripted star is intended to indicate that this is the number of
is the mass of Be carrier used in the process blank. The other symbols are as used above. The superscripted star is intended to indicate that this is the number of ![]() Be atoms in a particular blank, and not necessarily the summary value that should be used above in calculating the nuclide concentration in a particular sample (although it might be - see discussion below). The analytical uncertainty in the number of
Be atoms in a particular blank, and not necessarily the summary value that should be used above in calculating the nuclide concentration in a particular sample (although it might be - see discussion below). The analytical uncertainty in the number of ![]() Be atoms in the particular process blank is:
Be atoms in the particular process blank is:
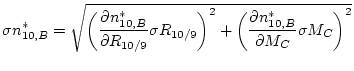 |
(12) |
where:
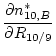 |
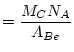 |
(13) |
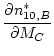 |
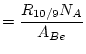 |
(14) |
Again,
![]() is the uncertainty in the measured
is the uncertainty in the measured ![]() Be/
Be/![]() Be ratio of the process blank, and
Be ratio of the process blank, and
![]() is the uncertainty in the mass of Be carrier added to the process blank.
is the uncertainty in the mass of Be carrier added to the process blank.
Having now calculated the number of atoms of ![]() Be in a particular process blank
Be in a particular process blank
![]() , there are two ways to think about what blank value to use in determining the nuclide concentration in a sample, depending on what you believe about the source of the
, there are two ways to think about what blank value to use in determining the nuclide concentration in a sample, depending on what you believe about the source of the ![]() Be contamination in the laboratory.
Be contamination in the laboratory.
One common way to think about this is to assume that all the samples in a particular batch are equally contaminated by unwanted ![]() Be atoms during processing. This would be true if these unwanted
Be atoms during processing. This would be true if these unwanted ![]() Be atoms came from sources that were common to all the samples in a batch. The simplest way to accomplish this would be if acids or other reagents were the source of the spurious
Be atoms came from sources that were common to all the samples in a batch. The simplest way to accomplish this would be if acids or other reagents were the source of the spurious ![]() Be. In fact, the way we have set up this procedure, we know this to be true in part, because some (if not most) of the unwanted
Be. In fact, the way we have set up this procedure, we know this to be true in part, because some (if not most) of the unwanted ![]() Be atoms come from the Be carrier, which is common to all the samples in the batch as well as the process blank that was processed along with them. This approach suggests that, when determining the nuclide concentration in a particular sample, the
Be atoms come from the Be carrier, which is common to all the samples in the batch as well as the process blank that was processed along with them. This approach suggests that, when determining the nuclide concentration in a particular sample, the ![]() Be blank that should be taken into account is precisely the amount that was measured in the process blank run together with that sample. In this case, the values of
Be blank that should be taken into account is precisely the amount that was measured in the process blank run together with that sample. In this case, the values of ![]() and
and
![]() that should be used in Equations 6 and 7 are the values of
that should be used in Equations 6 and 7 are the values of
![]() and
and
![]() calculated for the particular process blank that was run together in the same batch as your sample.
calculated for the particular process blank that was run together in the same batch as your sample.
The second way to think about this is to assume that the number of atoms of unwanted ![]() Be in each sample is different. This would be the case if contamination came from soil particles, or other dust particles enriched in atmospherically produced
Be in each sample is different. This would be the case if contamination came from soil particles, or other dust particles enriched in atmospherically produced ![]() Be that found their way into the lab; or if it came from cross-contamination between samples sometime during the chemical processing. If this were true, and we took the number of
Be that found their way into the lab; or if it came from cross-contamination between samples sometime during the chemical processing. If this were true, and we took the number of ![]() Be atoms and their measurement uncertainty for a single blank as representative of the unwanted
Be atoms and their measurement uncertainty for a single blank as representative of the unwanted ![]() Be atoms in all samples, we would risk using a blank uncertainty
Be atoms in all samples, we would risk using a blank uncertainty
![]() that was too small. The measurement uncertainty for a particular process blank would not take into account the fact that there might be a different number of unwanted
that was too small. The measurement uncertainty for a particular process blank would not take into account the fact that there might be a different number of unwanted ![]() Be atoms in the other samples in the batch. In this situation, it would be better to look at a series of process blanks run over a long period of time (as long as they were run using the same Be carrier solution). Then we would use the average and standard deviation of the long-term series of process blanks, instead of the value of any one blank, as the representative blank value and uncertainty to be applied to all of the samples run during this time.
Be atoms in the other samples in the batch. In this situation, it would be better to look at a series of process blanks run over a long period of time (as long as they were run using the same Be carrier solution). Then we would use the average and standard deviation of the long-term series of process blanks, instead of the value of any one blank, as the representative blank value and uncertainty to be applied to all of the samples run during this time.
Here's an example. Figure 1 shows a series of process blanks run over a 6-month period. All the process blanks contained the same amount of the same Be carrier, but the difference between blanks was much greater than the measurement precision of each individual blank. Eventually this problem was traced to unwanted ![]() Be atoms in the Al metal used to make the accelerator cathodes used to hold the Be samples for analysis, and it turned out that the number of spurious
Be atoms in the Al metal used to make the accelerator cathodes used to hold the Be samples for analysis, and it turned out that the number of spurious ![]() Be atoms that turned up in the measurement was extremely variable between cathodes. This indicated that the number of unwanted
Be atoms that turned up in the measurement was extremely variable between cathodes. This indicated that the number of unwanted ![]() Be atoms would be different for each sample, and that if we used the blank value and uncertainty measured for only the particular blank that was run in the same batch as a particular sample, we would underestimate the uncertainty in the sample nuclide concentration. Thus, for all the samples run during this period, it seemed best to use an
Be atoms would be different for each sample, and that if we used the blank value and uncertainty measured for only the particular blank that was run in the same batch as a particular sample, we would underestimate the uncertainty in the sample nuclide concentration. Thus, for all the samples run during this period, it seemed best to use an ![]() and
and
![]() derived from the average and standard deviation of all these blanks (
derived from the average and standard deviation of all these blanks (![]() = 45000 and
= 45000 and
![]() = 46000), instead of the measured value for any particular one of the blanks.
= 46000), instead of the measured value for any particular one of the blanks.