This procedure is essentially the same for ![]() Al. The only major difference in the chemical processing is that the quartz sample typically contains a relatively large amount of total Al, so it is not necessary to add Al carrier. Thus, the total number of atoms of stable
Al. The only major difference in the chemical processing is that the quartz sample typically contains a relatively large amount of total Al, so it is not necessary to add Al carrier. Thus, the total number of atoms of stable ![]() Al in the sample, here denoted
Al in the sample, here denoted ![]() , replaces the number of atoms of the stable nuclide added as carrier. This quantity is:
, replaces the number of atoms of the stable nuclide added as carrier. This quantity is:
 |
(15) |
where ![]() is the molar weight of Al (26.982 g
is the molar weight of Al (26.982 g ![]() mol
mol![]() ) and
) and ![]() is the mass of Al in the sample (g). The mass of Al in the sample is usually determined by ICP-OES or AA analysis of an aliquot taken immediately after the sample has been dissolved. The
is the mass of Al in the sample (g). The mass of Al in the sample is usually determined by ICP-OES or AA analysis of an aliquot taken immediately after the sample has been dissolved. The ![]() Al concentration in quartz,
Al concentration in quartz, ![]() , is then:
, is then:
where ![]() is the measured
is the measured ![]() Al/
Al/![]() Al ratio. The uncertainty
Al ratio. The uncertainty
![]() is:
is:
where:
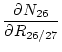 |
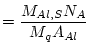 |
(18) |
 |
(19) | |
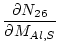 |
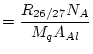 |
(20) |
One determines the process blank for ![]() Al measurements in the same way as for
Al measurements in the same way as for ![]() Be, as described above.
Be, as described above. ![]() Al is a much less common nuclide in the environment, so generally
Al is a much less common nuclide in the environment, so generally ![]() Al blanks are less important than
Al blanks are less important than ![]() Be blanks.
Be blanks.