The accelerator mass spectrometer actually measures the ratio ![]() of atoms of
of atoms of ![]() Be to atoms of
Be to atoms of ![]() Be in the target sample. The atoms of both isotopes that actually get to the accelerator can come from a variety of sources: they can be in the actual quartz sample itself, they can be in the
Be in the target sample. The atoms of both isotopes that actually get to the accelerator can come from a variety of sources: they can be in the actual quartz sample itself, they can be in the ![]() Be carrier that is added during chemical processing, or they can be unwanted atoms that arrive sometime during the chemical processing. Thus, the ratio
Be carrier that is added during chemical processing, or they can be unwanted atoms that arrive sometime during the chemical processing. Thus, the ratio ![]() is made up as follows:
is made up as follows:
Where ![]() is the number of atoms of
is the number of atoms of ![]() Be in the sample;
Be in the sample; ![]() is the number of atoms of
is the number of atoms of ![]() Be in the Be carrier (which is supposed to be pure
Be in the Be carrier (which is supposed to be pure ![]() Be, but in reality always contains some amount of
Be, but in reality always contains some amount of ![]() Be);
Be); ![]() is the number of atoms of
is the number of atoms of ![]() Be added accidentally during processing; and
Be added accidentally during processing; and ![]() ,
, ![]() and
and ![]() are the numbers of atoms of
are the numbers of atoms of ![]() Be that come from the same three sources.
Be that come from the same three sources.
Note: some AMS labs, Lawrence Livermore in particular, provide two isotope ratios in their results: an uncorrected ratio, and a `blank-corrected' ratio which takes into account one of the process blanks that the user submitted with their sample. The object of this document is to describe how to do the blank correction, so ![]() here refers to the isotope ratio that has not already had the process blank subtracted from it. AMS labs handle this differently in their results, so you should check to determine which value you have.
here refers to the isotope ratio that has not already had the process blank subtracted from it. AMS labs handle this differently in their results, so you should check to determine which value you have.
The quantity we actually want to know is the number of atoms per gram of quartz in the sample, which isn't in this equation yet. Call it ![]() , the capital
, the capital ![]() denoting a concentration in atoms
denoting a concentration in atoms ![]() g
g![]() rather than a number of atoms.
rather than a number of atoms. ![]() , the total number of atoms in the sample, is
, the total number of atoms in the sample, is
![]() , where
, where ![]() is the mass of the quartz sample (g). This makes Equation 1:
is the mass of the quartz sample (g). This makes Equation 1:
We can simplify this equation in two ways.
First, Be is a rare element in the environment, so (in nearly all cases), the amount of ![]() Be that is in the original sample and occurs from contamination in the lab is very much less than the relatively large amount of
Be that is in the original sample and occurs from contamination in the lab is very much less than the relatively large amount of ![]() Be that we add in the form of carrier. Basically,
Be that we add in the form of carrier. Basically,
![]() and
and
![]() , so
, so
![]() .
.
Second, the standard practice in nearly all laboratories is to use the same amount of ![]() Be carrier for all samples and all process blanks, that is, blanks that are subjected to the entire chemical extraction process in parallel with the samples. Thus, the number of atoms of
Be carrier for all samples and all process blanks, that is, blanks that are subjected to the entire chemical extraction process in parallel with the samples. Thus, the number of atoms of ![]() Be added with the carrier
Be added with the carrier ![]() will be the same for all samples and process blanks. Also, we have to assume that the number of atoms of
will be the same for all samples and process blanks. Also, we have to assume that the number of atoms of ![]() Be added accidentally during processing
Be added accidentally during processing ![]() will always be the same for all samples, at least within a particular batch of samples processed together. Thus, the quantity
will always be the same for all samples, at least within a particular batch of samples processed together. Thus, the quantity
![]() will always be the same for samples and process blanks, so we can simply call
will always be the same for samples and process blanks, so we can simply call
![]() , that is, the number of atoms of
, that is, the number of atoms of ![]() Be in a process blank. Section 4 below describes how to decide on a value for
Be in a process blank. Section 4 below describes how to decide on a value for ![]() .
.
With these two simplifications we have:
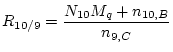 |
(3) |
The number of atoms of ![]() Be in the carrier
Be in the carrier ![]() is calculated from the mass of Be added as carrier:
is calculated from the mass of Be added as carrier:
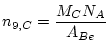 |
(4) |
where ![]() is the mass of Be added as carrier (g),
is the mass of Be added as carrier (g), ![]() is Avogadro's number (
is Avogadro's number (
![]() atoms
atoms ![]() mol
mol![]() ), and
), and ![]() is the molar weight of Be (9.012 g
is the molar weight of Be (9.012 g ![]() mol
mol![]() ). For example, most labs add 250
). For example, most labs add 250 ![]() g of
g of ![]() Be as carrier, which contains
Be as carrier, which contains
![]() =
=
![]() atoms of
atoms of ![]() Be.
Be.
This gives:
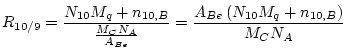 |
(5) |
which we can solve to get the formula for the quantity we actually want, ![]() :
: