The uncertainty in the ![]() Be concentration in the quartz sample must take into account three sources of uncertainty: the uncertainty in the isotope ratio measurement (which we will call
Be concentration in the quartz sample must take into account three sources of uncertainty: the uncertainty in the isotope ratio measurement (which we will call
![]() ), the uncertainty in the number of atoms in the process blanks (
), the uncertainty in the number of atoms in the process blanks (
![]() ), and the uncertainty in the mass of Be added as carrier (
), and the uncertainty in the mass of Be added as carrier (
![]() ). The isotope ratio uncertainty
). The isotope ratio uncertainty
![]() is supplied by the AMS lab. The blank uncertainty
is supplied by the AMS lab. The blank uncertainty
![]() is discussed below. The uncertainty in the Be carrier mass comes from the fact that the Be carrier is added in solution, and the Be concentration in the solution has some uncertainty. The uncertainty in the Be concentration in typical commercial Be solutions is about 1%, so the uncertainty in the Be carrier mass is typically
is discussed below. The uncertainty in the Be carrier mass comes from the fact that the Be carrier is added in solution, and the Be concentration in the solution has some uncertainty. The uncertainty in the Be concentration in typical commercial Be solutions is about 1%, so the uncertainty in the Be carrier mass is typically
![]() .
.
Using standard error-propagation methods, the formula for the uncertainty in the ![]() Be concentration in quartz, that is,
Be concentration in quartz, that is,
![]() , is:
, is:
where:
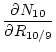 |
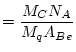 |
(8) |
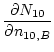 |
(9) | |
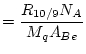 |
(10) |