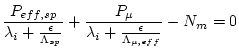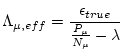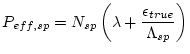


Next: make_al_be_consts_v2.m
Up: Wrapper scripts and control
Previous: get_al_be_age.m
Contents
results = get_al_be_erosion(sample,consts,nuclide)
This is the main control function that carries out the erosion rate calculation. al_be_erosion_one and
al_be_erosion_many call it.
The argument sample is a structure containing sample information. The fields are as follows:
| sample.sample_name |
Sample name |
string |
| sample.lat |
Latitude |
double |
| sample.long |
Longitude |
double |
| sample.elv |
elevation in meters |
double |
| sample.pressure |
pressure in hPa (optional if sample.elv is set) |
double |
| sample.aa |
Flag that indicates how to interpret the elevation value. |
string |
| sample.thick |
Sample thickness in cm |
double |
| sample.rho |
Sample density, g 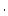 cm cm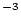 |
double |
| sample.othercorr |
Shielding correction. |
double |
| sample.N10 |
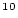 Be concentration, atoms Be concentration, atoms 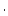 g g
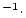 yr yr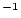 |
double |
| sample.delN10 |
standard error of  Be concentration Be concentration |
double |
| sample.N26 |
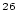 Al concentration, atoms Al concentration, atoms 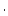 g g
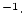 yr yr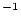 |
double |
| sample.delN26 |
standard error of 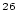 Al concentration Al concentration |
double |
The argument consts is a structure containing the constants. It is typically the structure created by
make_al_be_consts_v12.m, although only a subset of the fields in that structure are actually used by this function.
The argument nuclide tells the function which nuclide is being used; allowed values are 10 or 26. This is a numerical value, not a string.
This function returns a structure called results that contains the following fields:
| Non-scaling-scheme-specific information: |
| results.flags |
Non-fatal error messages, mostly to do with nuclide concentrations above saturation |
string |
| results.main_version |
Version number for this function |
string |
| results.obj_version |
Version of objective function called internally |
string |
| results.mu_version |
Version of P_mu_total called internally |
string |
| results.Pmu0 |
Surface production rate due to muons (atoms  g g
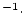 yr yr ) ) |
double |
| Scaling-scheme-specific information: |
| results.P_St |
Surface production rate due to spallation (atoms 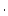 g g
 yr yr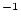 ) following non-time-dependent Lal (1991) - Stone(2000) scaling scheme ) following non-time-dependent Lal (1991) - Stone(2000) scaling scheme |
double |
| results.Egcm2yr |
1x5 vector containing erosion rates (g 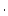 cm cm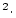 yr yr ) according to the St, De, Du, Li, and Lm scaling schemes respectively ) according to the St, De, Du, Li, and Lm scaling schemes respectively |
1 x 5 double |
| results.EmMyr |
1x5 vector containing erosion rates (m 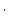 Myr Myr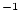 ) according to the St, De, Du, Li, and Lm scaling schemes respectively ) according to the St, De, Du, Li, and Lm scaling schemes respectively |
1 x 5 double |
| results.delE_int |
1x5 vector containing internal uncertainties (m  Myr Myr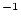 ) according to the 5 scaling schemes. Note that these should all be essentially equal. ) according to the 5 scaling schemes. Note that these should all be essentially equal. |
1 x 5 double |
| results.delE_ext |
1x5 vector containing external uncertainties (m 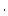 Myr Myr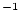 ) according to the 5 scaling schemes. ) according to the 5 scaling schemes. |
1 x 5 double |
| Diagnostic information: |
| results.fzero_status |
1x5 vector containing output flags returned by rootfinding function fzero at solving for the erosion rates from the 5 scaling schemes. |
1 x 5 double |
| results.fval |
1x5 vector containing objective function values (atoms  g g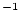 ) at the erosion rates from the 5 scaling schemes. ) at the erosion rates from the 5 scaling schemes. |
1 x 5 double |
| results.time_fzero |
1x5 vector containing the time (s) required for each solution. |
1 x 5 double |
| results.time_mu_precalc |
Time (s) required to calculate
 . . |
double |
1. Basic idea.
This function solves the equation:
![$\displaystyle \int^{\infty}_{0} \left[ P_{sp,0}(t)\exp \left(-\frac{\epsilon t}...
...t) + P_{\mu}(\epsilon t) \right] \exp{\left( -\lambda t \right)} dt - N_{m} = 0$](img231.png) |
(19) |
for the erosion rate 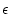 (here in g
(here in g 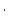 cm
cm
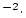 yr
yr ), where
), where
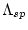 is the effective attenuation length for spallogenic production (g
is the effective attenuation length for spallogenic production (g 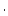 cm
cm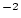 ),
), 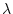 is the decay constant for the nuclide in question (yr
is the decay constant for the nuclide in question (yr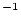 ),
), 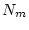 is the measured nuclide concentration (atoms
is the measured nuclide concentration (atoms 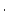 g
g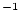 ),
),
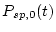 is the thickness-averaged surface nuclide production rate due to spallation as a function of time (atoms
is the thickness-averaged surface nuclide production rate due to spallation as a function of time (atoms  g
g
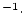 yr
yr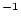 ), and
), and
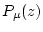 is the thickness-averaged production rate due to muons (atoms
is the thickness-averaged production rate due to muons (atoms 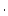 g
g
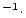 yr
yr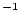 ) as a function of the depth
) as a function of the depth  (g
(g 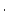 cm
cm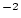 ) . As this cannot be solved analytically, we use the MATLAB rootfinding algorithm
) . As this cannot be solved analytically, we use the MATLAB rootfinding algorithm fzero to find the zero of an objective function, ET_objective.m, that computes the left-hand side of this equation, that is, the predicted nuclide concentration for a particular erosion rate less the measured nuclide concentration. The actual integration is described in the documentation for ET_objective.
2. Initial guess.
The objective function involves several numerical integrations, so finding its zero can be slow. The easiest way to speed it up is to provide it with an initial guess for the solution that is close to the actual solution. We do this by first estimating the erosion rate using the simple equation of Lal (1991), which disregards production by muons:
 |
(20) |
Here we calculate 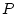 using the non-time-dependent St scaling scheme.
using the non-time-dependent St scaling scheme.
This can be solved directly for 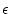 to obtain the initial guess.
to obtain the initial guess.
3. Calculate the production rates; pass to objective function; solve.
We then assemble the functions
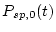 (for each scaling scheme) and
(for each scaling scheme) and
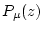 and pass them to the objective function, then find its zero to obtain the corresponding erosion rate for each scaling scheme.
and pass them to the objective function, then find its zero to obtain the corresponding erosion rate for each scaling scheme.
The actual assembly of
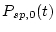 for the four time-dependent scaling schemes is the same as is used in
for the four time-dependent scaling schemes is the same as is used in get_al_be_age.m, and is described above in section 1.3.
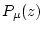 is generated on a 100-point log-spaced vector from 0 to
is generated on a 100-point log-spaced vector from 0 to
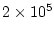 g
g  cm
cm using the function
using the function P_mu_total.m. The spacing of this vector affects the accuracy of the solution; this is discussed in more detail in the documentation for ET_objective.m.
4. Error propagation.
The fact that the full erosion rate equation cannot be solved analytically also makes error propagation difficult. We propagate errors linearly via the standard error propagation formula, but we cannot compute the derivatives of the derived erosion rate with respect to the uncertain input parameters, that are required in the formula, analytically, so two additional solutions of the full equation are required to estimate the partial derivative with respect to each uncertain parameter. It is time-consuming to do this using the full forward model, so we use a simplified erosion rate - nuclide concentration relationship for the uncertainty analysis:
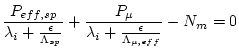 |
(21) |
where 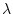 is the decay constant for the nuclide of interest,
is the decay constant for the nuclide of interest,
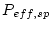 is the effective surface production rate due to spallation,
is the effective surface production rate due to spallation, 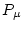 is the surface production rate due to muons,
is the surface production rate due to muons,
 is the effective attenuation length for production by spallation, and
is the effective attenuation length for production by spallation, and
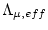 is the effective attenuation length for production by muons. Both
is the effective attenuation length for production by muons. Both
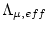 and
and
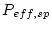 depend on the erosion rate, which is why this simplified equation cannot be used to accurately calculate the erosion rate in the first place. However, as we have already calculated
depend on the erosion rate, which is why this simplified equation cannot be used to accurately calculate the erosion rate in the first place. However, as we have already calculated 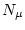 , the nuclide concentration attributable to production by muons, in the course of solving the full equation above, we can calculate the value of
, the nuclide concentration attributable to production by muons, in the course of solving the full equation above, we can calculate the value of
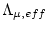 for which the simplified equation would yield the true erosion rate by:
for which the simplified equation would yield the true erosion rate by:
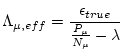 |
(22) |
where
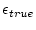 is the `true' erosion rate calculated by solving the full equation.
is the `true' erosion rate calculated by solving the full equation.
In like manner, we have already calculated 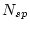 , the nuclide concentration attributable to production by spallation, so we can also calculate the value of
, the nuclide concentration attributable to production by spallation, so we can also calculate the value of
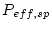 that would yield the correct erosion rate by:
that would yield the correct erosion rate by:
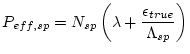 |
(23) |
Finally, the simplified erosion rate equation cannot be solved directly either, so it is coded as an internal function that can be used as an argument to fzero. We can then calculate the partial derivatives of the erosion rate with respect to the uncertain parameters
 ,
,
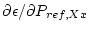 , etc. numerically by perturbing the input parameters and repeatedly solving the simple erosion rate equation. We use a first-order centered difference scheme.
, etc. numerically by perturbing the input parameters and repeatedly solving the simple erosion rate equation. We use a first-order centered difference scheme.
Finally, we use the resulting partial derivatives and input parameter uncertainties to evaluate the standard error propagation formula for internal and external uncertainties. Note that the internal uncertainty, that is, the uncertainty due to measurement error alone, is for all practical purposes the same for all the different scaling schemes. On the other hand, the external uncertainties, which reflect uncertainties in production rates as well, are different for each scaling scheme.



Next: make_al_be_consts_v2.m
Up: Wrapper scripts and control
Previous: get_al_be_age.m
Contents
2007-11-13
![$\displaystyle \int^{\infty}_{0} \left[ P_{sp,0}(t)\exp \left(-\frac{\epsilon t}...
...t) + P_{\mu}(\epsilon t) \right] \exp{\left( -\lambda t \right)} dt - N_{m} = 0$](img231.png)