stone2000Rcsp.m

Syntax:

scalingfactor = stone2000Rcsp(h,Rc)

Calculates the geographic scaling factor for cosmogenic-nuclide production with varying cutoff rigidity and atmospheric pressure. Uses an adaptation of the scheme in Stone (2000) and Lal (1991) that allows for higher values of cutoff rigidity than were permitted by the original scheme.

Relevant papers are:

Lal D., 1991. Cosmic ray labeling of erosion surfaces: in situ nuclide production rates and erosion models. Earth and Planetary Science Letters, v. 104, pp. 424-439.

Nishiizumi K., Winterer E.L., Kohl C.P., Klein J., Middleton R., Lal D., Arnold J.R., 1989. Cosmic ray production rates of $^{10}$Be and $^{26}$Al from glacially polished rocks. Journal of Geophysical Research 94. pp. 17,907-17.915.

Stone, J., 2000. Air pressure and cosmogenic isotope production. Journal of Geophysical Research 106, pp. 23,753-23,759.

The input arguments are h, atmospheric pressure (hPa) and Rc, cutoff rigidity (GV). Accepts either scalars or vectors of equal sizes for all the input arguments. Returns either a scalar or a vector of the appropriate size.

The function:

First, uses Equation (2) of Stone (2000) to calculate the scaling factor for spallation $S(R_{C},h)$ for the site atmospheric pressure, at index values of cutoff rigidity $R_{C}$ corresponding to the index latitudes used in the source paper. This equation is:

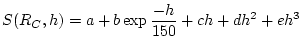$$S(R_{C},h) = a + b \exp{\frac{-h}{150}} + ch + dh^{2} + eh^{3}$$ (79)

Where the constants $a...e$ are defined for certain index cutoff rigidities:

$R_{C}$	a	b	c	d	e
14.9	31.8518	250.3193	-0.083393	7.4260e-5	-2.2397e-8
14.02	34.3699	258.4759	-0.089807	7.9457e-5	-2.3697e-8
11.62	40.3153	308.9894	-0.106248	9.4508e-5	-2.8234e-8
8.38	42.0983	512.6857	-0.120551	1.1752e-5	-3.8809e-8
5.13	56.7733	649.1343	-0.160859	1.5463e-5	-5.0330e-8
2.54	69.0720	832.4566	-0.199252	1.9391 e-5	-6.3653e-8
$<$ 0.93	71.8733	863.1927	-0.207069	2.0127e-5	-6.6043e-8

The index values of cutoff rigidity are simply the index latitudes given in the source paper, latitude $\theta$ having been transformed to cutoff rigidity $R_{C}$ by:

$$R_{C} = 14.9 \cos^{4}(\theta)$$ (80)

This is essentially the same as the method of correcting for paleomagnetic variation given in Nishiizumi et al. (1989), which is based on Equation 81.

Second, obtains the scaling factor at the particular value of $R_{C}$ at the site from the scaling factor - cutoff rigidity pairs at the index rigidities by linear interpolation. For cutoff rigidities greater than 14.9 GV, this requires extending the $S$- $R_{C}$ relationship to higher $R_{C}$. We do this by regressing the the highest three values of $\log R_{C}$ against the corresponding values of $\log S$ for the site atmospheric pressure, then using the resulting line in log-log space to extrapolate the scaling factor-rigidity relationship past 14.9 GV. Here is an example of the results of this procedure at various altitudes:

Basically we are assuming that the scaling factor decreases log-linearly with the cutoff rigidity at rigidities greater than 10 GV. This is a common first-order approximation in cosmic-ray physics texts - see, for example, Sandstrom. The important thing about this assumption is that in practice it is very rarely used - it is only necessary for low latitudes for several thousand years in the late Holocene - so whether it is or is not exact has minimal importance to the eventual result of nearly any exposure-age calculation.

We use log-log linear regression on the highest three $R_{C}$ values, instead of a direct extension of the highest two values, to smooth irregularities that result from the polynomial form of the Lal scaling factor curves.