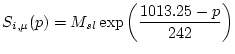


Next: stone2000Rcsp.m
Up: Subsidiary calculation functions
Previous: stdatm.m
Contents
Syntax:
scalingfactor = stone2000(latitude, pressure, fsp)
Calculates the geographic scaling factor for cosmogenic-nuclide production with varying latitude and altitude according to the scheme in:
Stone, J., 2000. Air pressure and cosmogenic isotope production. Journal of Geophysical Research 106, pp. 23,753-23,759.
The input arguments are latitude, the site latitude (decimal degrees), pressure, the atmospheric pressure at the site (hPa), and fsp the fraction of production due to neutron spallation (nondimensional). Accepts vector arguments. The argument fsp, if omitted, defaults to 0.978, which is the correct value for 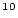 BeThe corresponding value for
BeThe corresponding value for 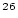 Al is 0.974. Note that using
Al is 0.974. Note that using fsp = 0.844 (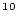 Be) and
Be) and fsp = 0.844 (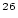 Al) will closely reproduce the scaling factors given in Lal (1991) as long as the standard atmosphere is used. Note also that this function can be made to yield the scaling factor for spallation only by specifying
Al) will closely reproduce the scaling factors given in Lal (1991) as long as the standard atmosphere is used. Note also that this function can be made to yield the scaling factor for spallation only by specifying fsp = 1 and the scaling factor for production by muons only by specifying fsp = 0.
The geographic production rate scaling factor 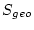 is:
is:
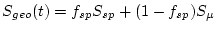 |
(76) |
where 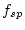 is the fraction of production due to spallation (input argument
is the fraction of production due to spallation (input argument fsp), 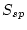 is the scaling factor for production by neutron spallation:
is the scaling factor for production by neutron spallation:
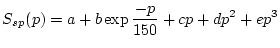 |
(77) |
and 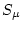 is the scaling factor for production by muons:
is the scaling factor for production by muons:
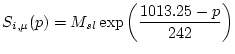 |
(78) |
Where the constants 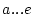 and
and 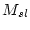 depend on the latitude and are defined for certain index latitudes:
depend on the latitude and are defined for certain index latitudes:
| Latitude |
a |
b |
c |
d |
e |
 |
| 0° |
31.8518 |
250.3193 |
-0.083393 |
7.4260e-5 |
-2.2397e-8 |
0.587 |
| 10° |
34.3699 |
258.4759 |
-0.089807 |
7.9457e-5 |
-2.3697e-8 |
0.600 |
| 20° |
40.3153 |
308.9894 |
-0.106248 |
9.4508e-5 |
-2.8234e-8 |
0.678 |
| 30° |
42.0983 |
512.6857 |
-0.120551 |
1.1752e-5 |
-3.8809e-8 |
0.833 |
| 40° |
56.7733 |
649.1343 |
-0.160859 |
1.5463e-5 |
-5.0330e-8 |
0.933 |
| 50° |
69.0720 |
832.4566 |
-0.199252 |
1.9391 e-5 |
-6.3653e-8 |
1.000 |
 60° 60° |
71.8733 |
863.1927 |
-0.207069 |
2.0127e-5 |
-6.6043e-8 |
1.000 |
This table duplicates Table 1 in Stone (2000).
This function actually calculates 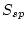 and
and 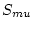 for index latitudes that bound the actual latitude of the site, and then determines the value at the site by linear interpolation. The exact method of interpolation used is relatively unimportant, but we have chosen linear interpolation to avoid the problem of under- and over-shooting between index latitudes due to the polynomial form of the Lal equations. Basically, linear interpolation guarantees that the scaling factor at the site is not outside the range of the scaling factors at the bounding index latitudes.
for index latitudes that bound the actual latitude of the site, and then determines the value at the site by linear interpolation. The exact method of interpolation used is relatively unimportant, but we have chosen linear interpolation to avoid the problem of under- and over-shooting between index latitudes due to the polynomial form of the Lal equations. Basically, linear interpolation guarantees that the scaling factor at the site is not outside the range of the scaling factors at the bounding index latitudes.



Next: stone2000Rcsp.m
Up: Subsidiary calculation functions
Previous: stdatm.m
Contents
2007-11-13