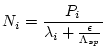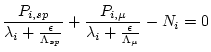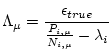

Next: make_al_be_consts_v12.m
Up: Wrapper scripts and control
Previous: get_al_be_age.m
results = get_al_be_erosion(sample,consts,nuclide)
This is the main control function that carries out the erosion rate calculation. al_be_erosion_one and
al_be_erosion_many call it.
The argument sample is a structure containing sample information. The fields are as follows:
| sample.sample_name |
Sample name |
string |
| sample.lat |
Latitude |
double |
| sample.long |
Longitude |
double |
| sample.elv |
elevation in meters |
double |
| sample.pressure |
pressure in hPa (optional if sample.elv is set) |
double |
| sample.aa |
Flag that indicates how to interpret the elevation value. |
string |
| sample.thick |
Sample thickness in cm |
double |
| sample.rho |
Sample density, g 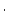 cm cm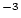 |
double |
| sample.othercorr |
Shielding correction. |
double |
| sample.N10 |
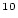 Be concentration, atoms Be concentration, atoms 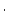 g g
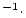 yr yr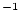 |
double |
| sample.delN10 |
standard error of 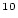 Be concentration Be concentration |
double |
| sample.N26 |
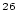 Al concentration, atoms Al concentration, atoms 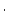 g g
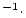 yr yr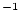 |
double |
| sample.delN26 |
standard error of 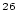 Al concentration Al concentration |
double |
The argument consts is a structure containing the constants. It is typically the structure created by
make_al_be_consts_v12.m, although only a subset of the fields in that structure are actually used by this function.
The argument nuclide tells the function which nuclide is being used; allowed values are 10 or 26. This is a numerical value, not a string.
This function returns a structure called results that contains the following fields:
| results.main_version |
Version number for this function |
string |
| results.obj_version |
Version number for the objective function used in solving for the erosion rate |
string |
| results.Egcm2yr |
Erosion rate (g 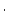 cm cm
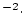 yr yr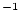 ) ) |
double |
| results.EmMyr |
Erosion rate (m 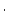 Myr Myr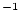 ) ) |
double |
| results.delE_int |
Internal uncertainty (m 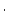 Myr Myr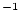 ) ) |
double |
| results.delE_ext |
External uncertainty (m 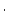 Myr Myr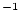 ) ) |
double |
| results.P0sp |
Thickness-integrated production rate due to spallation |
double |
| results.P0muneg |
Thickness-integrated production rate due to negative muon capture |
double |
| results.P0mufast |
Thickness-integrated production rate due to fast muon reactions |
double |
| results.Nsp |
Nuclide concentration attributable to production by spallation (atoms 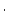 g g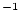 ) ) |
double |
| results.Nmu |
Nuclide concentration attributable to production by muons (atoms 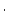 g g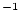 ) ) |
double |
| results.fzero_status |
Diagnostic flag indicating whether fzero converged or not |
double |
| results.fzero_output |
Structure containing diagnostic information supplied by fzero. See the MATLAB documentation of fzero for more information. |
|
| results.fval |
Value of objective function at solution |
double |
| results.time |
Time required to solve for the erosion rate (s) |
double |
This function solves the equation:
![$\displaystyle \int^{\infty}_{0} \left[ P_{i,sp}(\epsilon t) + P_{i,\mu f}(\epsilon t) + P_{i,\mu-}(\epsilon t) \right] e^{-\lambda_{i}t} dt - N_{i} = 0$](img35.png) |
(12) |
for the erosion rate 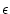 (here in g
(here in g  cm
cm
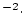 yr
yr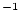 ), where
), where 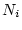 is the measured concentration of nuclide
is the measured concentration of nuclide 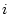 , and
, and
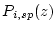 ,
,
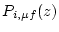 , and
, and
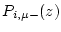 are the production rates of nuclide
are the production rates of nuclide 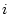 due to spallation, fast muon interactions, and negative muon capture, averaged over the sample thickness, as functions of depth. As this cannot be solved analytically, we use the MATLAB rootfinding algorithm
due to spallation, fast muon interactions, and negative muon capture, averaged over the sample thickness, as functions of depth. As this cannot be solved analytically, we use the MATLAB rootfinding algorithm fzero to find the zero of an objective function, al_be_E_forward.m, that computes the right-hand side of this equation, that is, the predicted nuclide concentration for a particular erosion rate. The actual integration is described in the documentation for al_be_E_forward.
As the objective function involves several numerical integrations, finding its zero can be slow. The easiest way to speed it up is to provide it with an initial guess for the solution that is close to the actual solution. We do this by first estimating the erosion rate using the simple equation of Lal (1991):
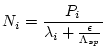 |
(13) |
and then scaling this result according to a set of comparisons between the Lal erosion rate and the true erosion rate that we have obtained from calculating both at a variety of erosion rates and elevations. This usually produces an initial guess for the erosion rate that is within a few percent of the actual solution of the full equation, with the result that solving the full equation takes 1-3 seconds on our server.
The fact that the full erosion rate equation cannot be solved analytically also makes error propagation difficult. We cannot compute the derivatives of the derived erosion rate with respect to the uncertain input parameters analytically, so it requires two additional solutions of the full equation to estimate the derivative with respect to each uncertain parameter. It is time-consuming to do this using the full equation, so we use a simplified erosion rate - nuclide concentration relationship for the uncertainty analysis:
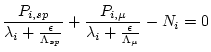 |
(14) |
where
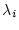 is the decay constant for nuclide
is the decay constant for nuclide 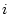 ,
, 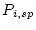 is the surface production rate due to spallation,
is the surface production rate due to spallation, 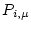 is the surface producrion rate due to muons,
is the surface producrion rate due to muons,
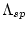 is the effective attenuation length for production by spallation, and
is the effective attenuation length for production by spallation, and
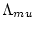 is the effective attenuation length for production by muons.
is the effective attenuation length for production by muons.
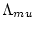 varies depending on the erosion rate and the sample elevation, which is why this simplified equation cannot be used to accurately calculate the erosion rate in the first place. However, as we have already calculated
varies depending on the erosion rate and the sample elevation, which is why this simplified equation cannot be used to accurately calculate the erosion rate in the first place. However, as we have already calculated 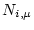 , the nuclide concentration attributable to production by muons, while solving the full equation above, we can calculate the value of
, the nuclide concentration attributable to production by muons, while solving the full equation above, we can calculate the value of
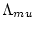 for which the simplified equation would yield the true erosion rate by:
for which the simplified equation would yield the true erosion rate by:
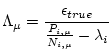 |
(15) |
where
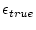 is the `true' erosion rate calculated by solving the full equation. The result is that the simplified erosion rate-nuclide concentration relationship is adequate for the uncertainty analysis. We have found that this simplified method of calculating the uncertainties yields uncertainties that, for all practical purposes, are the same as the `true' uncertainty obtained by numerically differentiating the full erosion rate equation, for the full physically reasonable range of erosion rates and sample locations.
is the `true' erosion rate calculated by solving the full equation. The result is that the simplified erosion rate-nuclide concentration relationship is adequate for the uncertainty analysis. We have found that this simplified method of calculating the uncertainties yields uncertainties that, for all practical purposes, are the same as the `true' uncertainty obtained by numerically differentiating the full erosion rate equation, for the full physically reasonable range of erosion rates and sample locations.
Thus, the simplified erosion rate equation is coded as a subfunction which can be solved quickly by fzero. This allows the derivatives of the erosion rate with respect to the uncertain parameters
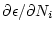 ,
,
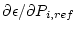 , etc. to be quickly calculated. We actually do this with a first-order centered difference scheme. We then add the uncertainties in quadrature to arrive at the final internal and external uncertainties.
, etc. to be quickly calculated. We actually do this with a first-order centered difference scheme. We then add the uncertainties in quadrature to arrive at the final internal and external uncertainties.


Next: make_al_be_consts_v12.m
Up: Wrapper scripts and control
Previous: get_al_be_age.m
2006-05-08
![$\displaystyle \int^{\infty}_{0} \left[ P_{i,sp}(\epsilon t) + P_{i,\mu f}(\epsilon t) + P_{i,\mu-}(\epsilon t) \right] e^{-\lambda_{i}t} dt - N_{i} = 0$](img35.png)