

Next: get_al_be_erosion.m
Up: Wrapper scripts and control
Previous: al_be_erosion_many.m
results = get_al_be_age(sample,consts,nuclide)
This is the main control function that carries out the exposure age calculation. al_be_age_one and
al_be_age_many call it.
The argument sample is a structure containing sample information. The fields are as follows:
| sample.sample_name |
Sample name |
string |
| sample.lat |
Latitude |
double |
| sample.long |
Longitude |
double |
| sample.elv |
elevation in meters |
double |
| sample.pressure |
pressure in hPa (optional if sample.elv is set) |
double |
| sample.aa |
Flag that indicates how to interpret the elevation value. |
string |
| sample.thick |
Sample thickness in cm |
double |
| sample.rho |
Sample density, g 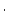 cm cm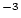 |
double |
| sample.othercorr |
Shielding correction. |
double |
| sample.E |
Erosion rate, cm 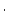 yr yr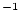 |
double |
| sample.N10 |
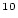 Be concentration, atoms Be concentration, atoms 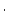 g g
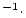 yr yr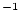 |
double |
| sample.delN10 |
standard error of 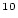 Be concentration Be concentration |
double |
| sample.N26 |
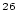 Al concentration, atoms Al concentration, atoms 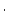 g g
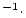 yr yr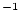 |
double |
| sample.delN26 |
standard error of 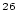 Al concentration Al concentration |
double |
The argument consts is a structure containing the constants. It is typically the structure created by
make_al_be_consts_v12.m, although only a subset of the fields in that structure are actually used by this function.
The argument nuclide tells the function which nuclide is being used; allowed values are 10 or 26. This is a numerical value, not a string.
This function returns a structure called results that contains the following fields:
| results.main_version |
Version number for this function |
string |
| results.simplet |
Exposure age (yr) |
double |
| results.delt_int |
Internal uncertainty (yr) |
double |
| results.delt_ext |
External uncertainty (yr) |
double |
| results.thick_sf |
Thickness correction |
double |
| results.simple_sf |
Geographic scaling factor |
double |
| results.Psp |
Thickness-integrated surface production rate due to spallation |
double |
| results.Pmu |
Thickness-integrated surface production rate due to muons |
double |
The exposure age calculation goes as follows:
Calculate the thickness scaling factor  by calling the function
by calling the function thickness.m.
If sample.pressure is not set, calculate it by calling either stdatm.m or antatm.m.
Calculate the geographic scaling factor 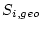 for nuclide
for nuclide 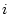 by calling the function
by calling the function stone2000.m.
The production rate of nuclide 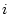 in the sample
in the sample 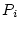 (atoms
(atoms 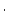 g
g
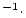 yr
yr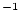 ) is :
) is :
 |
(5) |
where 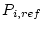 is the reference production rate for nuclide
is the reference production rate for nuclide 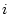 and
and 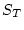 is the topographic shielding correction.
is the topographic shielding correction.
The exposure age 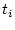 for nuclide
for nuclide 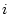 is then:
is then:
![$\displaystyle t_{i} = \frac{1}{\lambda_{i}+\frac{\rho \epsilon}{\Lambda_{sp}}} ...
...{P_{i}} \left( \lambda_{i}+\frac{\rho \epsilon}{\Lambda_{sp}} \right) \right] }$](img21.png) |
(6) |
where 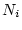 is the measured concentration of nuclide
is the measured concentration of nuclide 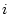 (atoms
(atoms 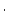 g
g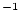 ),
), 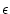 is the erosion rate (g
is the erosion rate (g 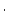 cm
cm
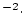 yr
yr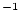 ),
),
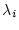 is the decay constant for nuclide
is the decay constant for nuclide 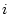 (yr
(yr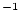 ),
),  is the sample density (g
is the sample density (g 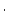 cm
cm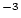 ), and
), and
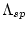 is the effective attenuation length for prodution by neutron spallation.
is the effective attenuation length for prodution by neutron spallation.
The internal uncertainty in the exposure age
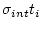 is:
is:
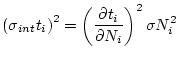 |
(7) |
where
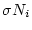 is the standard error in the measured nuclide concentration and:
is the standard error in the measured nuclide concentration and:
![$\displaystyle \frac{\partial t_{i}}{\partial N_{i}} = \left[ P_{i} - N_{i} \left( \lambda_{i}+\frac{\rho \epsilon}{\Lambda_{sp}} \right) \right]^{-1}$](img29.png) |
(8) |
The external uncertainty in the exposure age
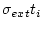 is:
is:
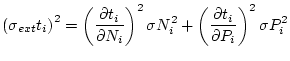 |
(9) |
where
![$\displaystyle \frac{\partial t_{i}}{\partial P_{i}} = -N_{i} \left[ P_{i}^{2} -...
..._{i} \left( \lambda_{i}+\frac{\rho \epsilon}{\Lambda_{sp}} \right) \right]^{-1}$](img32.png) |
(10) |
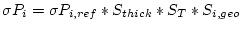 |
(11) |
and
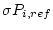 is the standard error in the reference production rate of nuclide
is the standard error in the reference production rate of nuclide 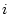 .
.


Next: get_al_be_erosion.m
Up: Wrapper scripts and control
Previous: al_be_erosion_many.m
2006-05-08
![$\displaystyle t_{i} = \frac{1}{\lambda_{i}+\frac{\rho \epsilon}{\Lambda_{sp}}} ...
...{P_{i}} \left( \lambda_{i}+\frac{\rho \epsilon}{\Lambda_{sp}} \right) \right] }$](img21.png)
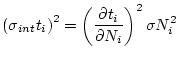
![$\displaystyle \frac{\partial t_{i}}{\partial N_{i}} = \left[ P_{i} - N_{i} \left( \lambda_{i}+\frac{\rho \epsilon}{\Lambda_{sp}} \right) \right]^{-1}$](img29.png)
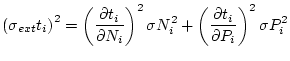
![$\displaystyle \frac{\partial t_{i}}{\partial P_{i}} = -N_{i} \left[ P_{i}^{2} -...
..._{i} \left( \lambda_{i}+\frac{\rho \epsilon}{\Lambda_{sp}} \right) \right]^{-1}$](img32.png)