MATLAB code for geometric cosmic-ray shielding calculations
MATLAB code for geometric cosmic-ray shielding calculations
Greg Balco
Berkeley Geochronology Center
1 Introduction
This document describes MATLAB code used for computing obstruction of the surface cosmic ray flux by oddly shaped objects. The purpose of this is to enable calculation of the production rate of a cosmic-ray-produced nuclide for surface exposure dating applications. This software ingests i) a shape file describing one or more objects that obstruct the cosmic-ray flux, and ii) coordinates of a location where the production rate is to be determined. It uses many simplifying assumptions about cosmic-ray particle transport and a Monte Carlo integration to determine what fraction of the total cosmic-ray flux reaches the sample location.
The present document describes the operation of the software. Theory and applications are covered in an accompanying paper:
Balco, G., 2012 in review. Simplified computer code for estimating cosmic-ray shielding due to oddly shaped objects. Quaternary Geochronology.
This software was written to facilitate exposure-dating of precariously balanced rocks useful for earthquake hazard estimates. These rocks are formed by subsurface weathering and gradually exposed at the surface by downwasting of surrounding weathered rock and sediment. Thus, this software is designed to compute cosmic-ray shielding either due to a free-standing obstruction by itself, or due to the obstruction as well as a layer of soil or sediment that buries the sample location and partially or fully buries the obstruction.
Section 2 describes a graphical user interface to the software. Section 3 describes the individual MATLAB functions that perform computations and enable the GUI.
2 Graphical user interface
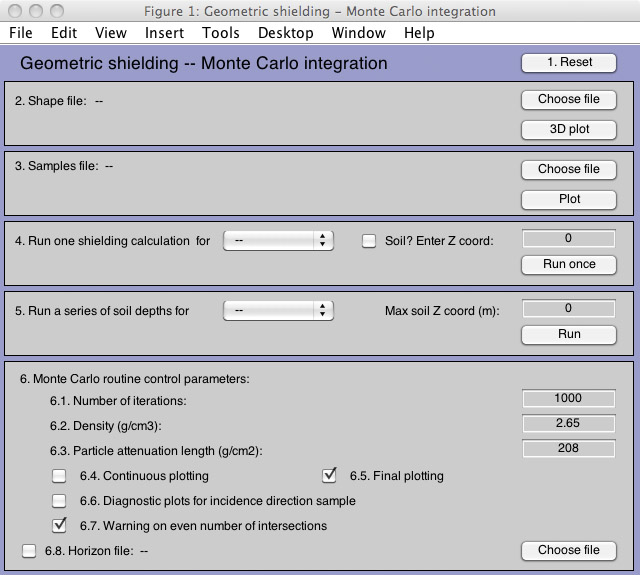
A graphical user interface is provided by executing the m-file shielding_control_window.m. This action clears existing MATLAB windows and draws a new window entitled "Geometric shielding - Monte Carlo integration." See Figure 1. Controls in this window are numbered and described in the subsections below.
|
|
Figure 1: Main control window.
|
2.1 `1. Reset' button.
The button marked "1. Reset" in the upper right corner of the main control window clears all MATLAB figures other than this one, clears all filenames, and sets all user-settable entry fields to default values.
2.2 `2. Shape file' section.
This section of the main control window specifies the shape file that defines the objects whose shielding effect we are computing.
The "Choose file" button pops a dialog box enabling one to select this file. Typically, this file is a .stl file (it can also be a .mat-file that is the result of processing a .stl file - see additional discussion below). The .stl format consists of a text file describing a series of triangular facets that together make up a three-dimensional object. A binary version of the .stl format exists; only the text version is used here. This file format is commonly used to define 3D objects for rapid prototyping or computer-aided manufacturing purposes. Here is an example of a .stl file entitled "temp.stl" and defining two facets:
solid [C:\Users\balcs\Documents\temp.stl]
facet normal 0.00 0.00 0.00
outer loop
vertex -4.957786 -2.770371 0.602929
vertex -4.896107 -2.830239 0.808729
vertex -4.975159 -2.737364 0.196783
endloop
endfacet
facet normal 0.00 0.00 0.00
outer loop
vertex -5.194063 -3.575649 -0.017283
vertex -5.434190 -3.412690 -0.130366
vertex -5.042836 -3.470916 -0.059296
endloop
endfacet
endsolid
Obviously, this format assumes a cartesian coordinate system. For purposes of this software, the z direction should be vertical and the vertices should be defined in units of meters. The cosmic-ray flux is assumed to be isotropic with respect to compass direction, so if the object is exposed to the cosmic-ray flux from the entire upper hemisphere, the x- and y- axes do not have to be pointed in any particular direction. However, if the far-field horizon seen by the object is obstructed and you intend to use this horizon information in the calculation (see below), then the x-direction of the shape model coordinate system should be oriented to the direction defined as north (zero azimuth) in the horizon definition.
Some software that uses .stl files utilizes the order that the vertices of each facet are specified to define an ïnside" and öutside" for each facet, i.e. the vertices are in clockwise order when viewed from the outside of the object. This software does not pay attention to vertex order.
The calculation scheme in this software assumes two things: first, the shape file defines one or more closed objects, and second, one is computing cosmic-ray shielding for a point that lies within one of these objects. This corresponds to the typical geological situation in which one has collected a sample from the surface of the object that has some thickness; thus, the effective center of the sample (the `effective center' is the point where the production rate is equal to the average production rate in the entire sample) lies inside the original outline of the object by approximately half the sample thickness. Given these assumptions, a simulated cosmic ray trajectory originating from infinite distance will pass through an odd number of facets before arriving at the sample point. If the software observes an even number of intersections, it notifies the MATLAB command window and assumes that that ray path experienced complete attenuation. This convention allows one to simplify the shape file by defining a number of öne-sided" objects near the sample location that represent the land surface and would in fact fully obstruct the cosmic-ray flux originating from that direction. Thus, an option to turn off this error message is provided. On the other hand, an odd number of facet intersections could signal any one of a number of topological errors in the shape model or the sample location. Of course, this software provides no diagnostic capability to find or fix these errors.
Code to read in .stl files is in the m-file readstl.m. This action can be a bit time-consuming if the .stl file is long and requires a lot of text reads. To speed this up, one can use readstl.m to read the facet data in the .stl file into the workspace, then save this as a MATLAB binary (.mat) file. One can then specify the .mat file instead of the .stl file in this section. The following lines will read in a .stl file once and save as a .mat file that will be correctly read:
facetsRaw = readstl('../rocks/rock_1.stl');
save rock_1 facetsRaw;
The result of calling readstl must be saved under the variable name facetsRaw for this to work.
The "3D plot" button creates a new figure window showing a 3D plot of the object(s) defined in the shape file. The plotting code is located in the m-file plotFacets.m. To change the appearance of the plot, edit this file.
2.3 `3. Samples file' section and samples window.
This section of the main control window specifies the file that defines the location of the samples of interest for shielding calculations.
2.3.1 "Choose File" button
The "Choose file" button brings up a dialog box enabling file selection. Sample locations are defined in a text file in .csv (comma-separated values) format. Each line of the file defines the x,y,z location of the sample in the same coordinate system as the shape model. There is no other information in the file. Here is an example of a file defining sample locations:
-4.7780,-3.5856,0.6780
-5.0656,-3.6482,0.1990
-5.1252,-3.4671,-0.3220
The code for this function is mostly in the m-file loadSamples.m.
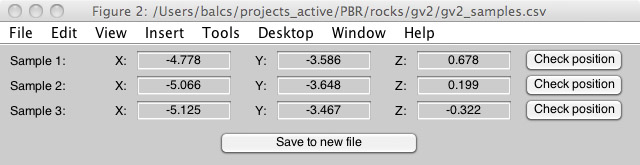
2.3.2 The samples window
Loading the file creates a new figure window whose title is the file name. Figure 2 shows an example of the figure window corresponding to the sample file above.
|
|
Figure 2: Samples window.
|
This window has two main features. First, it displays the sample locations in editable text boxes. Thus, you can adjust the sample locations. The values that appear in this window are the controlling values for the rest of the software - all subsequent calculations use whatever values appear in the samples window.
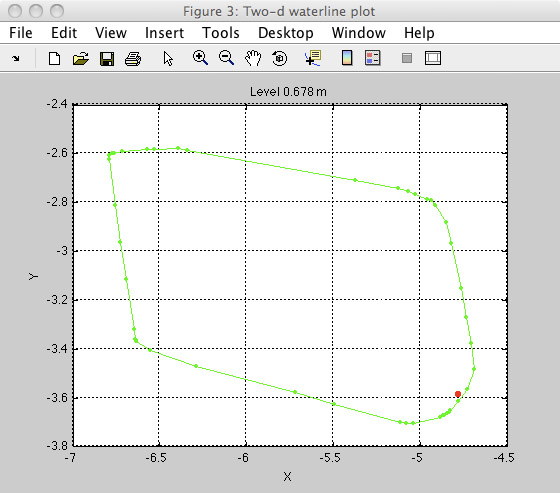
Second, the "Check position" buttons allow one to check the location of the samples with respect to the shape model. They bring up a new figure window showing a horizontal section through the shape model at the z-value of the sample. This permits you to check that the samples lie inside an object defined in the shape model. Figure 3 shows an example of one of these plots. Code for this function is in the m-files check_position.m and waterline.m.
|
|
Figure 3: Window showing a horizontal slice through a shape model at the z-value defined for a sample location. Green lines are sections through facets of the shape model; dots are intersections of facets; red dot is sample location. This shows that the sample is in fact located slightly inside the object defined by the shape model.
|
Finally, the "Save to new file" button allows one to save modified sample locations in a new .csv file. Typically the workflow here would be as follows. First, use photogrammetric software to define locations of samples on the surface of the object. Second, load this initial sample file and use the "Check position" buttons and the editable boxes in the samples window to adjust the sample locations to be the correct distance inside the object surface. Third, save the adjusted sample locations as a new .csv file and proceed with calculations.
2.3.3 "Plot" button
This button creates a new figure window containing a 3D plot of the shape model and the sample locations. If a figure window created by the `3D plot' button in the `shape file' section already exists, the samples will be plotted in this window. The plotting code is located in the m-files plotFacets.m and plotSamples.m. Edit these files to change the appearance of the plot.
2.4 `4. Run one shielding calculation' section.
This section carries out a single shielding calculation. Assuming a shape file and a samples file have already been specified, one must choose a sample number from the dropdown menu. Once a sample file has been loaded, the dropdown contains the numbers of available samples. Sample numbers match those in the samples window, which in turn simply follow the order that samples are listed in the .csv file.
This section also provides the option to carry out the shielding calculation with the assumption that the object defined in the shape model is partially buried by soil. This feature exists because the original application of this software was to compute the cosmic-ray shielding of samples collected from precariously balanced rocks useful for seismic hazard estimation. These rocks form by exhumation from beneath a layer of weathered rock or soil, so it is necessary to compute the time-dependent shielding factor that results from this process. The checkbox labeled "Soil?" enables this feature. If this is enabled, one must enter the elevation of the soil surface in the same coordinate system as the shape model and samples. That is, enter the z-coordinate of the soil surface , not the thickness of soil above the sample site. If one enters a soil height that is below the sample height, it will be ignored.
The "Run" button carries out the shielding calculation and reports the results to the MATLAB command window. Checkboxes lower in the main control window (see Section 2.6 below) allow one to specify what figures are generated during the calculation.
2.5 `5. Run a series of soil depths' section.
This section carries out a number of shielding calculations in which the soil surface is assumed to be at different depths above a single sample. Thus, this computes the variation in shielding as the object defined in the shape model is exhumed. Again, this feature is designed for computing time-dependent shielding of precariously balanced rocks that are gradually exhumed from a layer of weathered rock or soil.
Again, one must select a sample from the dropdown menu. In addition, one must specify the maximum height of the soil surface in the text box marked "Max soil z coord". As in the previous section, one must specify a soil height in meters, in the same coordinate system as the shape model, not a soil thickness above the sample. In the precariously balanced rock example, this would correspond to the highest point on the rock - once the rock was entirely buried, then the surface would be completely flat and the shielding could be calculated in the normal, simple, fashion.
The software chooses the number of intermediate depths to achieve a spacing of something on the order of 10 cm. However, the number will always be at least 5.
The "Run" button carries out the calculation and reports results to the MATLAB command window. Results include the shielding factor estimates for the various soil heights as well as the zero-intercept (S0,i) and attenuation length (Li) of an exponential curve fit to the shielding-soil thickness relationship. These two parameters are needed for the application to precariously balanced rocks. For more discussion of this, see:
Balco G., Purvance M., Rood D., 2011. Exposure dating of precariously balanced rocks. Quaternary Geochronology 6, pp. 295-303.
Balco G., Purvance M., Rood D., 2012. Corrigendum to "Exposure dating of precariously balanced rocks." Quaternary Geochronology 9, p. 86.
Checkboxes lower in the main control window (see Section 2.6 below) enable or disable various plots and figures generated during this calculation.
2.6 `6. Monte Carlo routine control parameters' section.
This section of the main control window allows the user to change various default values and enable or disable various plots, figures, and error messages.
2.6.1 6.1. Number of iterations. This controls the number of iterations used in the Monte Carlo integration. If the horizon around the object of interest is unobstructed, 1000 iterations is usually adequate to converge on a stable estimate. If a significant fraction of the horizon is obstructed (see 6.8 below) then the number of iterations should be increased accordingly (because iterations with an obstructed ray path are disregarded and not replaced). The default value is 1000. If `final plotting' (see below) is checked, a convergence plot will be generated that helps in determining if there were enough iterations.
2.6.2 6.2. Density. This specifies the density of the objects defined in the shape file in units of g cm−3. Soil burying the objects is assumed to have the same density as the objects themselves. The default value is 2.65 g cm−3.
2.6.3 6.3. Particle attenuation length. This specifies the attenuation length for a single cosmic ray particle passing through rock (Λp; units of g cm−2). Note that this is not the same as the commonly used efffective attenuation length for cosmogenic nuclide production beneath a flat surface, that is usually represented by Λ and commonly taken to be near 160 g cm−2. The relationship between these two is approximately Λp=1.3Λ (Dunne et al., 1999). The default value for Λp is 208 g cm−2, which is equivalent to Λ = 208 gm cm−2.
2.6.4 6.4 Continuous plotting. This checkbox generates a figure at the beginning of the calculation showing the shape model, the sample location, the location of each cosmic ray generated in the Monte Carlo integration, the facets intersected by that ray, and the part of each ray which lies within rock or soil. The figure is updated for each iteration of the Monte Carlo iteration, which makes the calculation much slower. However, this is useful as a diagnostic tool to make sure the code is doing more or less what you think it should be doing. The default for this option is off.
2.6.5 6.5 Final plotting. This generates two plots at the end of the calculation. The default for this option is on.
One plot is similar to that generated by the `Continuous plotting' option, showing the shape model, the sample location, all the cosmic rays generated in the Monte Carlo integration, and the portion of each ray which lies within rock or soil. Again, this is a useful diagnostic tool to make sure the code is going what it should be doing.
The other plot shows the cumulative average shielding factor for each iteration. As more iterations are completed, the shielding factor is likewise averaging the results of more iterations, and thus converges on the correct overall estimate. This plot is useful for making sure that one is using enough iterations.
2.6.6 6.6 Diagnostic plots for incidence direction sample. This generates plots of the distribution of the randomly generated cosmic ray incidence directions. One is a polar-type plot showing the upper hemisphere; one is an x-y plot showing azimuth vs. horizon angle. In both plots, simulated cosmic rays that are excluded by a far-field horizon are shown in a different color. This is useful for making sure the software is correctly interpreting a far-field horizon. The default for this option is off.
2.6.7 6.7 Warning on even number of intersections. This enables a warning to be dumped to the command window when a simulated cosmic ray intersects an even number of facets in the shape model. The default value is on. As discussed above, this is not expected if all objects in the shape model are closed and the sample location lies within one of them. Thus, an even number of intersections might signal an error in the shape model or the sample location.
However, when this condition occurs, the software assumes that that cosmic ray is completely attenuated. Thus, one might set up the shape model to exploit this feature by defining a number of one-sided objects to represent objects that are thick enough to completely stop the cosmic-ray flux. In this situation, the error message would just be annoying, so there is an option to turn it off.
2.6.8 6.8. Horizon file. This provides the option to define a far-field horizon surrounding the sample site below which no cosmic rays are admitted to the calculation. The checkbox turns this option on and off. If this box is checked, one must also use the "Choose file" button to select a text file containing information about the horizon. This file should contain four lines. First, a line of azimuths (0-360 degrees) defining points on the horizon. These are numerical values separated by spaces. Second, a line of corresponding horizon angles (0-90 degrees) for the same points, again as space-separated numerical values. The third and fourth lines allow one to assume that the object of interest occupies the center of an infinite dipping surface; the third line gives the strike and the fourth line the dip. The third and fourth lines are optional.
For more information on the method of specifying the horizon, see:
http://hess.ess.washington.edu/math/general/skyline_input.php
Also see the file unpackHorizonFile.m.
Example horizon files follow:
1. A file specifying a horizon as well as strike and dip of the landscape surface:
20 40 56 100 300
0 10 5 12 0
150
30
2. A file specifying a horizon only:
20 40 56 100 300
0 10 5 12 0
3. A file specifying the strike and dip of the landscape surface only:
0
0
150
30
3 MATLAB function documentation
3.1 Primary calculation functions
3.1.1 generate_cosmic_rays.m
out = generate_cosmic_rays(numits,d)
This function generates a set of random cosmic ray incidence directions for Monte Carlo integration. They are distributed uniformly in azimuth and zenith angle in the upper hemisphere.
There is also the option to include a far-field horizon below which no cosmic rays will be generated. This option requires the function skyline.m from the online exposure age calculators at http:
hess.ess.washington.edu. skyline.m should be included in this distribution.
Input arguments:
numits is the number of randomly generated incidence directions desired.
d is an optional data structure that may or may not include several things. All fields are optional.
| d.plotFlag | Enter 0 (default) for no plotting, 1 to make diagnostic plots. |
| d.az | Azimuths of far-field horizon. See skyline.m for input format details. This field and the next three behave as described in skyline.m. Default is no far-field horizon. |
| d.el | Elevations of far-field horizon. See skyline.m for input format details. Default is no far-field horizon. |
| d.strike | Strike of far-field dipping surface. See skyline.m for input format details. Default is no far-field horizon. |
| d.dip | Dip of far-field dipping surface. See skyline.m for input format details. Default is no far-field horizon. |
The output argument has four fields:
| out.xyz | Matrix representing randomly generated incidence directions as vectors. Has three columns [x y z] and a number of rows equal to numits. |
| out.phi | Vector of length numits that contains zenith angles corresponding to the vectors in out.xyz. This facilitates later application of the zenith angle dependence of the intensity. |
| out.theta | Vector of length numits that contains corresponding azimuths. |
| out.ok | Vector of length numits that contains zero if the ray in question is obstructed by a far-field horizon, and one if it is not obstructed. If no far-field horizon was entered, contains all ones. |
3.1.2 readstl.m
out = readstl(fname);
This function reads in a .stl shape file containing a triangular facet representation of an object and returns the facets defined in a compact matrix form. Only recognizes the "facet" definition in .stl files. This function is not overly smart: i) it doesn't try to allocate correct amount of memory in advance; ii) there is no error or consistency checking; and iii) it should preserve CW/CCW orientation of facts, but doesn't care about this property of facets so doesn't check to make sure.
The input argument fname is a string containing the filename of the .stl file.
The output argument out is an n x 9 matrix where n is the number of facets defined in the .stl file. Each row is a facet: [x1 y1 z1 x2 y2 z2 x3 y3 z3], where vertex i has coords (xi,yi,zi).
Thus, a facet defined as follows in the .stl file:
facet normal 0.00 0.00 0.00
outer loop
vertex -5.194063 -3.575649 -0.017283
vertex -5.434190 -3.412690 -0.130366
vertex -5.042836 -3.470916 -0.059296
endloop
endfacet
is stored as:
[−5.194063 −5.434190 −5.042836 −3.575649 −3.412690 −3.470916 −0.017283 −0.130366 −0.059296]
This arrangement of values is basically chosen for convenience in use of the intersectLinePlane.m function.
3.1.3 shielding_loop.m
out = shielding_loop(in)
This function performs a Monte Carlo integration to compute shielding of the cosmic ray flux by an obstruction.
Uses the function intersectLinePlane.m from the `geom3d' toolbox by David Legland, which is available on the MATLAB File Exchange. This should also be included in this distribution.
The input argument in is a structure with the following required and optional fields.
Required fields:
| in.fname | Filename of file containing boulder geometry. This can be either a .stl file (in which case it calls readstl.m) or a .mat file resulting from a previous call to readstl.Coordinates of the shape file should be in meters. |
| in.thispoint | Vector [x y z] of sample point in same coordinate system as the .stl or .mat file. |
| in.rays.xyz | Matrix with orientation of cosmic rays to be evaluated, in the form returned by generate_cosmic_rays.m, which is x-y-z triples on the unit sphere. See generate_cosmic_rays.m. Normally this would be a large number of randomly generated values returned by generate_cosmic_rays, but having it as a parameter allows any arbitrary test set of rays to be evaluated. |
| in.rays.phi | Corresponding vector of zenith angles for these rays (as these have already been calculated by generate_cosmic_rays, it saves time to pass rather than recalculating from xyz data). |
| in.rays.ok | Corresponding vector showing which rays pass a far-field horizon. See generate_cosmic_rays.m. If there is no far-field horizon, then this is just a vector of ones. |
Optional fields to override defaults:
| in.plotFlag | Default 0 for no plotting, set to 1 for continuous plotting of each ray as the calculation proceeds. |
| in.finalPlotFlag | Default 0 for no plotting, set to 1 for summary and diagnostic plots after calculation completes. |
| in.rho | Rock density (g cm−3). Default is 2.65. |
| in.selv | Soil surface elevation (z-value) in same coordinate system as the shape file. Default is that the soil surface is below the sample location, i.e. there is no soil cover. |
| in.tpal | Particle attenuation length (g cm−2). Default is 208. |
| in.evenMessage | Flag to disable (0) or enable (1) warning message when a ray passes through an even number of facets. See discussion below. |
| in.ax | Angular distribution scaling exponent. Default is 2.3. |
The output argument out is the (scalar, nondimensional) shielding factor calculated by averaging the attenuation values computed for all iterations of the Monte Carlo integration. This is the ratio of the production rate at the obstructed sample site to the production rate at an unshielded site at the same location.
Notes:
1. All coordinates (for the shape file, sample location, and soil surface elevation) must be in meters.
2. The calculation expects that the sample location is inside one of the objects defined in the .stl file, and that all of these objects are closed. Then the ray should intersect either one facet (if it goes directly to the sample without passing through any additional obstructions) or (1 + 2n) facets (if it passes through n other objects before getting to the sample site). Thus, we expect it to intersect an odd number of facets. If it intersects an even number, we assume that the farthest-from-the-sample facet is the side of an infinitely large object, such that the sample is fully shielded from a ray with that incidence direction. This is a convenient way to set up .stl files to include only partial coverage of very large objects (like a mountainside), but an even number of intersections could also be caused by lots of undesired topological errors. Thus, when this condition occurs, the code i) sets the shielding factor for that ray to 0 (completely shielded, because this is desired for an infinitely large object), and ii) throws a warning message to the command window. To disable these messages (i.e. if you expect even numbers of intersections and you are OK with the above) then set in.evenMessage = 0.
3. Soil is taken to have the same density as rock.
4. The vector in.rays.ok that reflects far-field shielding should be calculated such that the far-field horizon is referenced to the same coordinate system as the shape model. That is, azimuth 0 in the horizon definition should be in the x-direction of the shape model. Specifically, this is because generate_cosmic_rays.m uses the function sph2cart to generate azimuths from vector triples.
3.2 Functions related to the graphical user interface and/or used for plotting results
3.2.1 check_position.m
out = check_position(a);
This function is part of the graphical user interface to the Monte Carlo integration shielding calculation. It plots a horizontal slice through a volume to aid in determining whether or not a sample is within a PBR.
The input argument a is the number of the sample to plot. Then, this function gets information from the `samples' window to obtain the sample location.
The output argument returns the handle to the new figure generated.
3.2.2 loadSamples.m
loadSamples(fname);
This function is part of the graphical user interface to the Monte Carlo integration shielding calculation. It loads a sample data file (in .csv form) and creates a window with sample information.
The input argument fname is a string with the name of the sample data file. The sample data file is a .csv text file containing a line with x,y,z coordinates for each sample.
The output argument is not used.
3.2.3 plotFacets.m
out = plotFacets(facetsRaw)
This function is part of the graphical user interface to the Monte Carlo integration shielding calculation. It plots facets derived from a .stl file into a 3D plot window.
The input argument facetsRaw is a matrix containing information about the facets, in the form output by readstl.m.
The output argument is not used.
3.2.4 plotSamples.m
This function is part of the graphical user interface for Monte Carlo integration of cosmic-ray shielding calculations. It reads sample data out of the "samples" window and plots it into a window showing a 3-d plot of the shielding object.
Has no arguments.
3.2.5 shielding_control_window.m
When called with no argument, this function initializes the graphical user interface for Monte Carlo integration of cosmic-ray shielding calculations. When called with a string argument, it implements callbacks for the various GUI objects.
3.2.6 unpackHorizonFile.m
unpackHorizonFile(fname);
This function is part of the graphical user interface for Monte Carlo integration of cosmic-ray shielding calculations. It reads in a text file containing horizon information and returns a variable structure containing the information in the text file.
Input argument fname is a string containing the filename to read.
Output argument out has fields:
| out.az | Vector of horizon azimuths. |
| out.el | Corresponding vector of horizon elevations. |
| out.strike | Strike of far-field dipping surface |
| out.dip | Dip of far-field dipping surface |
These fields are in the form needed by skyline.m.
The input file has two or four lines:
1. Azimuths separated by spaces (if none, line reads 0)
2. Elevations separated by spaces (if none, line reads 0)
3. Value of strike (optional)
4. Value of dip (optional)
Example horizon files follow:
1. A file specifying a horizon as well as strike and dip of the landscape surface:
20 40 56 100 300
0 10 5 12 0
150
30
2. A file specifying a horizon only:
20 40 56 100 300
0 10 5 12 0
3. A file specifying the strike and dip of the landscape surface only:
0
0
150
30
3.2.7 waterline.m
out = waterline(facetsRaw,level,d)
This function generates a horizontal ring (i.e., a "waterline") around a faceted volume at a given elevation. Used for checking the location of sample points relative to the object surface.
Input arguments:
facetsRaw is a matrix defining a faceted volume. It is the output of readstl.m.
level is the level at which to draw the line, in the same coordinate system as facetsRaw.
d is an optional structure with fields:
| d.plotRock | 0 no plot, 1 plots a 3-d view of the entire object with the waterline. |
| d.plotLevel | 0 no plot, 1 plots x-y plot of volume x-section at z = level. |
| d.tryToSort | 0 returns unsorted line segments for each facet intersected; 1 attempts to sort line segments into a single continuous line. Only set to 1 if you are pretty sure you have a single closed volume at the desired elevation; otherwise the results may be very strange. This part of the code could be greatly improved. On the other hand, it's not really relevant to the main point of this software. |
Output argument out is a structure with fields:
| out.unsorted | nx2 matrix with n/2 pairs of [x y] rows, each of which defines a line segment. No particular order to the line segments. |
| out.sorted | nx2 matrix with rows [x y] defining the waterline at level. This field only exists if d.tryToSort = 1. |
File translated from
TEX
by
TTH,
version 4.03.
On 18 Sep 2013, 15:08.
|


