az and el are vectors containing the azimuths (degrees; 0 Syntax:
[out,data,ver] = skyline(az,el,strike,dip)
This function calculates the topographic shielding correction to the cosmic-ray flux at a site whose horizon is obstructed either by a dipping surface or by the surrounding topography.
The input arguments strike and dip are the strike and dip of the sampled surface in degrees.
The input arguments az and el are vectors containing the azimuths (degrees; 0 ![]() az
az ![]() 360; north = 0) and horizon angles (degrees; 0
360; north = 0) and horizon angles (degrees; 0 ![]() el
el ![]() 360; zenith = 90) of points on the horizon.
360; zenith = 90) of points on the horizon.
out is the shielding correction for the sample (nondimensional; the ratio of the nuclide production rate at the shielded site to the nuclide production rate at an unshielded site at the same location).
data is a vector containing the interpolated horizon angle visible to the sample, in degrees, for 1-degree increments of azimuth. It can be used to plot the horizon, e.g., plot(0:360,data)
ver is a string variable containing the version number of the function.
The calculation goes as folllows:
First, we divide the range of azimuths
![]() into 1-degree increments.
into 1-degree increments.
Second, we calculate the horizon angle ![]() of the dipping surface as a function of azimuth:
of the dipping surface as a function of azimuth:
| (73) |
where
![]() is the dip and
is the dip and ![]() is the strike of the surface.
is the strike of the surface.
Third, we interpolate the supplied horizon points to give the horizon angle of the topography as a function of azimuth.
Fourth, at each increment of azimuth, we take the higher of the horizon angle due to the dipping surface or the horizon angle due to the surrounding topography to be the horizon angle visible to the sample. This results in a vector
![]() which defines the visible horizon angle
which defines the visible horizon angle ![]() at each increment of azimuth
at each increment of azimuth ![]() .
.
Finally, the fraction of the cosmic-ray flux ![]() that lies below the horizon angle in the increment of azimuth at
that lies below the horizon angle in the increment of azimuth at ![]() is:
is:
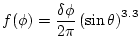 |
(74) |
where
![]() is the width of the azimuth increment in radians (
is the width of the azimuth increment in radians (![]() ). The total fraction of the cosmic-ray flux that lies below the horizon
). The total fraction of the cosmic-ray flux that lies below the horizon ![]() is the sum of the values of
is the sum of the values of ![]() for each increment of
for each increment of ![]() . The topographic shielding correction is then
. The topographic shielding correction is then ![]() .
.