z is depth below the surface in g Syntax:
out = P_mu_total(z,h,consts,dflag)
This function calculates the nuclide production rate due to muons at a particular surface elevation and depth below the surface. The method is described in:
Heisinger, B., Lal, D., Jull, A.J.T., Kubik. P., Ivy-Ochs, S., Neumaier, S., Knie, K., Lazarev, V., and Nolte, E., 2002. Production of selected cosmogenic radionuclides by muons: 1. Fast muons. Earth and Planetary Science Letters 200, pp. 345-355. (henceforth, H2002a).
Heisinger, B., Lal, D., Jull, A.J.T., Kubik. P., Ivy-Ochs, S., Knie, K., and Nolte, E., 2002. Production of selected cosmogenic radionuclides by muons: 2. Capture of negative muons. Earth and Planetary Science Letters 200, pp. 357-369. (henceforth, H2002b).
The input argument z is depth below the surface in g ![]() cm
cm![]() . This argument can be a vector.
. This argument can be a vector.
The input argument h is the atmospheric pressure at the surface in hPa.
The input argument consts is a structure containing nuclide-specific constants. The fields are as follows:
| consts.Natoms | number density of target atoms in quartz | atoms |
| consts.k_neg | summary yield for production by negative muon capture in quartz | atoms |
| consts.sigma190 | measured cross-section at 190 GeV for production by fast muon reactions | cm |
The argument dflag is a string variable telling the function what to return. If dflag = `no,' the output is simply a vector of production rates of the same size as the input argument z. If dflag = `yes,' the output is a structure containing diagnostic information, as follows:
| out.phi_vert_slhl | Flux of vertically traveling muons at the specified depths at sea level | muons |
| out.R_vert_slhl | Stopping rate of vertically traveling muons at the specified depths at sea level | muons |
| out.phi_vert_site | Flux of vertically traveling muons at the specified depths at the site elevation | muons |
| out.R_vert_site | Stopping rate of vertically traveling muons at the specified depths at the site elevation | muons |
| out.phi | Total flux of muons at the specified depths at the site elevation | muons |
| out.R | Total stopping rate of negative muons at the specified depths at the site elevation | negative muons |
| out.Beta | Factor describing the energy dependence of fast muon reaction cross-sections | nondimensional |
| out.Ebar | Mean muon energy at the specified depths | GeV |
| out.P_fast | Nuclide production rate by fast muon reactions at the specified depths | atoms |
| out.P_neg | Nuclide production rate by negative muon capture at the specified depths | atoms |
| out.H | Atmospheric depth between the site elevation and sea level | g |
| out.LZ | Atmospheric attenuation lengths for vertically traveling muons stopping at the specified depths | g |
The calculation goes as follows.
1. Calculate the flux of vertically traveling muons as a function of depth at sea level and high latitude.
This is accomplished by Equations (1) and (2) in H2002a. The flux of vertically traveling muons at a depth ![]() at sea level and high latitude
at sea level and high latitude
![]() is:
is:
![$\displaystyle \Phi_{v,0}(z) = \frac {5.401 \times 10^{7}} {\left( z + 21000 \ri...
...+1000 \right) ^{1.66} + 1.567 \times 10^{5} \right] } e^{-5.5 \times 10^{-6} z}$](img593.png) |
(42) |
for depths
![]() g
g ![]() cm
cm![]() . This is Equation (1) from H2002a, modified so that
. This is Equation (1) from H2002a, modified so that ![]() is in g
is in g ![]() cm
cm![]() . For greater depths,
. For greater depths,
![]() is given by Equation (2) of H2002a, similarly modified:
is given by Equation (2) of H2002a, similarly modified:
![$\displaystyle \Phi_{v,0}(z) = 1.82 \times 10^{-6} \left[ \frac{121100}{z} \right] ^{2} e^{- \frac{z}{121100}} + 2.84 \times 10^{-13}$](img601.png) |
(43) |
The units of
![]() are muons
are muons ![]() cm
cm
![]() s
s
![]() sr
sr![]() .
.
2. Calculate the stopping rate of vertically traveling muons as a function of depth at sea level and high latitude, which is equivalent to the range spectrum of vertically traveling muons at the surface.
The stopping rate of vertically traveling muons at a depth ![]() at sea level and high latitude
at sea level and high latitude
![]() is the derivative of the flux of vertically traveling muons with respect to depth. It has units of muons
is the derivative of the flux of vertically traveling muons with respect to depth. It has units of muons ![]() g
g
![]() s
s![]() . For depths
. For depths
![]() g
g ![]() cm
cm![]() ,
,
![$\displaystyle R_{v,0}(z) = \frac{d}{dz} \left( \Phi_{v,0}(z) \right) = -5.401\t...
...}{dz} - a \left( \frac{db}{dz}c + \frac{dc}{dz}b \right) } {b^{2}c^{2}} \right]$](img615.png) |
(44) |
where
| (45) | ||||
| (46) | ||||
| (47) |
The negative sign is added because the muon flux decreases with increasing depth, so its derivative ought properly to be negative, but we would like a positive value for the stopping rate. For greater depths,
![$\displaystyle R_{v,0}(z) = \frac{d}{dz} \left( \Phi_{v}(z) \right) = -1.82 \times 10^{-6} \left[ \frac{df}{dz} g + \frac{dg}{dz} f \right]$](img628.png) |
(48) |
where
![$\displaystyle = \left[ \frac{121100}{z} \right]^{2}$](img630.png) |
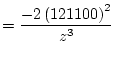 |
(49) | ||
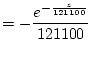 |
(50) |
The stopping rate of vertically traveling muons as a function of depth is equivalent to the range spectrum of vertically traveling muons at the surface. That is, a muon that had a range of 1000 g ![]() cm
cm![]() at the surface will stop at a depth of 1000 g
at the surface will stop at a depth of 1000 g ![]() cm
cm![]() .
.
3. Adjust the range spectrum of vertically traveling muons to a different elevation.
First, calculate the difference in atmospheric pressure between sea level and the elevation of interest. We use the standard atmosphere approximation to convert elevation to atmospheric pressure. The atmospheric pressure in hPa as a function of elevation is:
![$\displaystyle P_{atm}(z) = P_{atm,0} exp \left( -\frac{0.03417}{0.0065} \left[ \ln{288.15} -\ln{\left( 288.15 - 0.0065 h \right)} \right] \right)$](img641.png) |
(51) |
where ![]() is the elevation in meters and
is the elevation in meters and
![]() hPa is the sea level pressure. Pressure can then be converted to the quantity of interest, that is,
hPa is the sea level pressure. Pressure can then be converted to the quantity of interest, that is, ![]() , the atmospheric depth in g
, the atmospheric depth in g ![]() cm
cm![]() between the site of interest and sea level, by
between the site of interest and sea level, by
![]() .
.
If the atmospheric depth between sea level and the site of interest is ![]() , then the vertically traveling muon flux at the surface as a function of muon range
, then the vertically traveling muon flux at the surface as a function of muon range ![]() at sea level
at sea level
![]() can be scaled to the vertically traveling muon flux at the surface as a function of muon range at the site
can be scaled to the vertically traveling muon flux at the surface as a function of muon range at the site ![]() by:
by:
where
![]() is a range-dependent, that is, energy-dependent effective atmospheric attenuation length. These attenuation lengths are measured in studies of atmospheric muon fluxes. We follow H2002b and use a relation between muon momentum
is a range-dependent, that is, energy-dependent effective atmospheric attenuation length. These attenuation lengths are measured in studies of atmospheric muon fluxes. We follow H2002b and use a relation between muon momentum ![]() and effective attenuation length
and effective attenuation length
![]() derived from:
derived from:
Boezio, M, and 33 co-authors, 2000. Measurement of the flux of atmospheric muons with the CAPRICE94 apparatus. Physical Review D, 62, 032007.
The relation is:
| (53) |
In order to use this relation, we convert muon range to momentum using tabulated values in:
Groom, D.E., Mokhov, N.V., and Striganov, S.I., 2001. Muon stopping power and range tables 10 MeV - 100 TeV. Atomic data and nuclear data tables 78, pp. 183-356.
Having obtained
![]() for muons stopping at the depths of interest, we can then obtain the range spectrum of vertically traveling muons at the surface at the site of interest,
for muons stopping at the depths of interest, we can then obtain the range spectrum of vertically traveling muons at the surface at the site of interest, ![]() , which is equivalent to the muon stopping rate as a function of depth at the site of interest
, which is equivalent to the muon stopping rate as a function of depth at the site of interest ![]() , by applying Equation 53.
, by applying Equation 53.
4. Latitudinal variability in the range spectrum.
Although the muon range spectrum is expected to change with latitude as well as elevation due to geomagnetic effects, this effect is expected to be small. We follow H2002b and ignore it.
5. Calculate the flux of vertically traveling muons at the site of interest as a function of depth.
The flux of vertically traveling muons as a function of depth at the site of interest
![]() is the integral of the muon stopping rate as a function of depth at the site of interest
is the integral of the muon stopping rate as a function of depth at the site of interest ![]() , which we have just calculated, from infinite depth to depth
, which we have just calculated, from infinite depth to depth ![]() . That is, the muon flux at a particular depth is composed of all the muons which stop below that depth. Thus, the flux of vertically traveling muons as a function of depth at the site of interest
. That is, the muon flux at a particular depth is composed of all the muons which stop below that depth. Thus, the flux of vertically traveling muons as a function of depth at the site of interest
![]() is:
is:
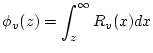 |
(54) |
We actually do this integral numerically, although it would be possible to obtain an analytical expression. We take the limit of integration to be
![]() g
g ![]() cm
cm![]() , where the muon flux is essentially negligible for our purposes.
, where the muon flux is essentially negligible for our purposes.
6. Calculate the total muon flux as a function of depth at the site of interest.
Following equations (3) - (5) in H2002a, the zenith angle dependence of the muon flux is:
where ![]() is the zenith angle and
is the zenith angle and ![]() is given by Equation (4) in H2002a, modified so that
is given by Equation (4) in H2002a, modified so that ![]() is given in g
is given in g ![]() cm
cm![]() :
:
| (56) |
The total muon flux at a particular depth ![]() then consists of Equation 56 integrated over the entire upper hemisphere and has units of muons
then consists of Equation 56 integrated over the entire upper hemisphere and has units of muons ![]() cm
cm![]() s
s![]() . This is given by:
. This is given by:
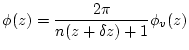 |
(57) |
7. Calculate the total muon stopping rate as a function of depth at the site of interest.
The total muon stopping rate as a function of depth ![]() is the derivative with respect to depth of the total muon flux as a function of depth
is the derivative with respect to depth of the total muon flux as a function of depth ![]() , that is:
, that is:
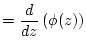 |
(58) | |
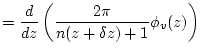 |
(59) | |
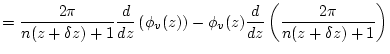 |
(60) | |
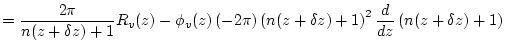 |
(61) | |
![$\displaystyle = \frac{2\pi}{n(z+\delta z)+1} R_{v}(z) - \phi_{v}(z) \left(-2\pi...
...-0.297 \times 10^{-2}}{\frac{z+\delta z}{100}+42} + 1.21 \times 10^{-5} \right]$](img687.png) |
(62) |
which, as we have already calculated ![]() ,
, ![]() , and
, and
![]() , we can calculate easily. Again, a factor of -1 is added to obtain a positive number of stopped muons.
, we can calculate easily. Again, a factor of -1 is added to obtain a positive number of stopped muons.
To summarize, we have now calculated the total muon flux ![]() (muons
(muons ![]() cm
cm
![]() s
s ![]() ) and the total stopping rate of muons
) and the total stopping rate of muons ![]() (muons
(muons ![]() g
g
![]() s
s ![]() ) at our site. We convert these to muons
) at our site. We convert these to muons ![]() cm
cm
![]() yr
yr ![]() and muons
and muons ![]() g
g
![]() yr
yr ![]() , respectively, by multiplying them by
, respectively, by multiplying them by
![]() s
s ![]() yr
yr![]() .
.
Finally, we compute the stopping rate of negative muons
![]() (negative muons
(negative muons ![]() g
g
![]() yr
yr ![]() ).
).
8. Calculate the nuclide production rate due to negative muon capture.
Following Equation (11) in H2002b, the production rate of nuclide ![]() (atoms
(atoms ![]() g
g
![]() yr
yr![]() ) from negative muon capture
) from negative muon capture
![]() is:
is:
| (63) |
where
| (64) | ||||
| (65) | ||||
| (66) |
9. Calculate the nuclide production rate due to fast muon reactions.
Following Equation (14) in H2002a, the production rate of nuclide ![]() (atoms
(atoms ![]() g
g
![]() yr
yr![]() ) from fast muon interactions
) from fast muon interactions
![]() is:
is:
where
![]() .
.
![]() is the nominal zero-energy muon interaction cross-section for the reaction responsible for producing nuclide
is the nominal zero-energy muon interaction cross-section for the reaction responsible for producing nuclide ![]() . Here is has units of cm
. Here is has units of cm![]() . The muon interaction cross-section for a particular reaction is thought to depend on the muon energy as follows:
. The muon interaction cross-section for a particular reaction is thought to depend on the muon energy as follows:
| (68) |
![]() is determined from the measured cross-sections
is determined from the measured cross-sections
![]() at 190 GeV energy in Table 1 of H2002a using this equation. These values for
at 190 GeV energy in Table 1 of H2002a using this equation. These values for ![]() Be and
Be and ![]() Al are:
Al are:
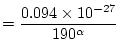 |
 |
(69) |
![]() is the number density of atoms of the target element (atoms
is the number density of atoms of the target element (atoms ![]() g
g![]() ). The values for O and Si relevant to
). The values for O and Si relevant to ![]() Be and
Be and ![]() Al production respectively are:
Al production respectively are:
| (70) |
where ![]() is a function of depth and is approximated by Equation (16) of H2002a:
is a function of depth and is approximated by Equation (16) of H2002a:
| (71) |
and
![]() is the mean muon energy at depth
is the mean muon energy at depth ![]() and is given by Equation (11) of H2002a:
and is given by Equation (11) of H2002a:
| (72) |