Syntax:
scalingfactor = desilets2006sp(h,Rc)
Calculates the geographic scaling factor for cosmogenic-nuclide production for particular cutoff rigidity and atmospheric pressure according to the scheme in:
Desilets D., Zreda M., Prabu T., 2006. Extended scaling factors for in situ cosmogenic nuclides: New measurements at low latitude. Earth and Planetary Science Letters, v. 246, pp. 265-276.
The input arguments are h, atmospheric pressure (hPa), and Rc, cutoff rigidity (GV). Accepts vector arguments.
This function:
Converts atmospheric pressure ![]() (hPa) to atmospheric depth
(hPa) to atmospheric depth ![]() (g
(g ![]() cm
cm![]() ) by
) by
![]() .
.
Assigns cutoff rigidities below 2 GV a value of 2 GV.
Obtains the effective attenuation length in air
![]() via Equation (4) in the source paper:
via Equation (4) in the source paper:
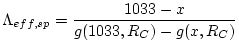 |
(26) |
where ![]() is the cutoff rigidity (GV) and the function
is the cutoff rigidity (GV) and the function
![]() is:
is:
| (27) | |||
![$\displaystyle \frac{1}{2} \left[ a_{0} + a_{1}R_{C} + a_{2}R_{C}^2\right] x^{2}$](img407.png) |
(28) | ||
![$\displaystyle \frac{1}{3} \left[ a_{3} + a_{4}R_{C} + a_{5}R_{C}^2\right] x^{3}$](img409.png) |
(29) | ||
![$\displaystyle \frac{1}{5} \left[ a_{6} + a_{7}R_{C} + a_{8}R_{C}^2\right] x^{4}$](img411.png) |
(30) |
given constants:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Obtains the altitude scaling factor ![]() :
:
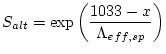 |
(31) |
Obtains the latitude scaling factor ![]() via Equation (6) in the source paper:
via Equation (6) in the source paper:
| (32) |
where ![]() is the cutoff rigidity,
is the cutoff rigidity,
![]() , and
, and
![]() .
.
Finally, obtains the total scaling factor
![]() .
.
Accepts either scalars or vectors of equal sizes for all the input arguments. Returns either a scalar or a vector of the appropriate size.