al_be_E_forward.m

out = al_be_E_forward(x,sample,consts,target,dflag)

This is the objective function used by get_al_be_erosion to solve for the erosion rate.

The argument x is the erosion rate.

The argument sample is a structure containing abbreviated information about the sample. The fields are as follows:

sample.thickgcm2	Sample thickness (g $\cdot$ cm$^{-2}$)	double
sample.pressure	Atmospheric pressure at sample location (hPa)	double

The argument consts contains nuclide-specific constants. The fields are as follows:

consts.l	decay constant	yr$^{-1}$
consts.Lsp	effective attenuation length for production by spallation	g $\cdot$ cm$^{-2}$
consts.Psp0	surface production rate by spallation at sample site	g $\cdot$ cm$^{-2}$
consts.Natoms	number density of target atoms in quartz	atoms $\cdot$ g$^{-1}$
consts.k_neg	summary yield for production by negative muon capture in quartz	atoms $\cdot$ (stopped $\mu_{-}$)$^{-1}$
consts.sigma190	measured cross-section at 190 GeV for production by fast muon reactions	cm$^{-2}$

The argument target is the measured nuclide concentration (atoms $\cdot$ g$^{-1}$), that is, the target that the objective function is trying to match.

The argument dflag is a string variable telling the function what to return. If dflag = `no,' the output is just the objective function value. If dflag = `yes,' the output is a structure containing diagnostic information, as follows:

out.ver	Version number of this function	string
out.N_mu	Nuclide concentration in sample attributable to production by muons at the given erosion rate	atoms $\cdot$ g$^{-1}$
out.N_sp	Nuclide concentration in sample attributable to production by spallation at the given erosion rate	atoms $\cdot$ g$^{-1}$
out.P_fast	Thickness-integrated nuclide production rate by fast muon reactions	atoms $\cdot$ g $^{-1} \cdot$ yr$^{-1}$
out.P_neg	Thickness-integrated nuclide production rate by negative muon capture	atoms $\cdot$ g $^{-1} \cdot$ yr$^{-1}$
out.P_sp	Thickness-integrated nuclide production rate by spallation	atoms $\cdot$ g $^{-1} \cdot$ yr$^{-1}$

This function calculates the following:

$$\int^{\infty}_{0} P_{i,sp}(\epsilon t)e^{-\lambda_{i}t} dt + \int... ...mu f}(\epsilon t) + P_{i,\mu-}(\epsilon t) \right] e^{-\lambda_{i}t} dt - N_{i}$$ (16)

where $\epsilon$ is the erosion rate (the input argument x, here in g $\cdot$ cm $^{-2} \cdot$ yr$^{-1}$), $N_{i}$ is the measured concentration of nuclide $i$ (the input argument target), and $P_{i,sp}(z)$, $P_{i,\mu f}(z)$, and $P_{i,\mu-}(z)$ are the production rates of nuclide $i$ due to spallation, fast muon interactions, and negative muon capture, averaged over the sample thickness, as functions of depth.

The first term of this equation, that is, the nuclide concentration in the sample attributable to production by spallation, can be integrated analytically:

$$\int^{\infty}_{0} P_{i,sp}(\epsilon t)e^{-\lambda_{i}t} dt = \fra... ...mbda_{sp}} \right) } \left[ 1 - \exp{ - \frac{\delta z}{\Lambda_{sp}} } \right]$$ (17)

where $P_{i,sp}(0)$ is the surface production rate of nuclide $i$ due to spallation (atoms $\cdot$ g $^{-1} \cdot$ yr$^{-1}$ ), $\Lambda_{sp}$ is the effective attenuation length for production by spallation (g $\cdot$ cm$^{-2}$), $\delta z$ is the sample thickness (g $\cdot$ cm$^{-2}$), and $\lambda_{i}$ is the decay constant for nuclide $i$ (yr$^{-1}$).

The second term must be calculated numerically. This function uses the MATLAB numerical integration algorithm quad to do the integral:

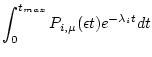$$\int^{t_{max}}_{0} P_{i,\mu}(\epsilon t) e^{-\lambda_{i}t} dt$$ (18)

where $P_{i,\mu} = P_{i,\mu f} + P_{i,\mu-}$ is calculated by the function P_mu_total.m. The upper limit of integration $t_{max}$ is either $(2 \times 10^{5}) / \epsilon$ (nuclide production is insignificant below $2 \times 10^{5}$ g $\cdot$ cm$^{-2}$) or five half-lives of the relevant nuclide (a negliible number of atoms produced before this time will still be present), whichever is smaller. The integration tolerance is set at $(1 \times 10^{-4})N_{i}$.